Project Euler : Problem 15 『Lattice paths』

Path / allenthepostman

問題

　左上をスタート、右下をゴールとした格子がある。
20×20の格子の場合、最短経路は何通りあるか。

1 × 1と2 × 2の場合

　はるか昔、先輩に「これ分からん。ponge君、教えてーや」って聞かれたような……？
あの時どうしたのか全く思い出せん。

　とりあえず、各格子点を座標と考えて、到達する経路が何通りあるか書いてみる。
f:id:pongeponge:20161103233618j:plain
1×1の時は左上の(0, 0)を1として、右(1, 0)は1、下(0, 1)は1、
上と左からゴール(1, 1)に到達する組み合わせは2通りで2。

　2×2の場合はこんな感じ。
f:id:pongeponge:20161103233649j:plain
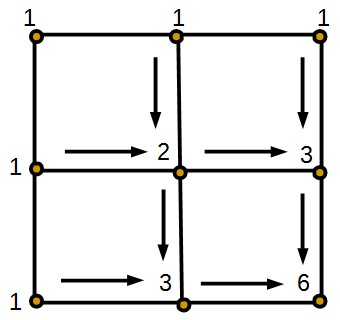
見てて気づくのは、
(1) 上端 y = 0と左端x = 0の座標は必ず1
(2) それ以外の(x, y)は(x-1, y)と(x, y-1)の和

1次元配列でやるか

　3×3の場合を考える。
3つの箱(配列)を用意して、全部に1を入れる
[1][1][1]
これをy = 0、つまり上端(y = 0)とする。
3×3の上端を表現するなら箱4つ必要なのでは？と思うけど、どうせ左端1だから省く！

　まず、左端(x = 1)に1を加える
[1+1][1][1] → [2][1][1]
次(x = 2)は、x = 1の値を加える。簡単に言うと、左隣を足す。
[2][2+1][1] → [2][3][1]
x = 3も同じようにする。
[2][3][3+1] = [2][3][4]
これでy=1が終了。
同じことを Y = 3になるまでくりかえす。

・y = 2
[2+1][3][4] → [3][3][4] → [3][3+3][4] → [3][6][4] → [3][6][6+4] → [3][6][10]

・y = 3
[3+1][6][10] → [4][6][10] → [4][6+4][10] → [4][10][10] → [4][10][10+10] → [4][10][20]

　y = 3まで計算が終われば、x = 3の値から3×3の最短経路数20が得られる。
それさえ分かれば、あとは20×20に拡張するだけ。

もっと簡単に求められないかな

　ペョーンと数式一発でOK！みたいになるといいんだけど…
と思ってノートを見たり見なかったりしてたら、何か数字の並びに見覚えが。

「あっ、これピタゴラスの三角数や！」

パスカルの三角形

　素で盛大に間違えたので検索に引っかからなくて難儀した。
~~大体三角形ぽいのは全部ピタゴラスのせい。~~
パスカルの三角形*1っていうのは、要はこういうやつ。

　　　　１
　　　１　１
　　１　２　１
　１　３　３　１
１　４　６　４　１

　これ、ちょっと斜めにして見れば2×2の各格子点の経路数そのもの(太字部分)。
丁寧にWikipediaには、上からn段目、左からk番目の数の求め方も載ってる。
じゃぁ上から何段目がグリッド数に対応してて、左から何番目が最短経路数になってるのか。

グリッド数とパスカルの三角形内の位置

　上から3段目、左から2番目(n, k) = (3, 2)が1×1に、
上から5段目、左から3番目(n, k) = (5, 3)が2×2の最短経路数に対応してる。
ということはグリッド数をg×gとすると、(n, k) = (2g+1, g+1)になってると予想できる。

　上記のパスカルの三角形をさらに続ければ分かるが、
3×3の場合、すなわち(n, k) = (2×3+1, 3+1)= (7, 4)が20に対応していて合ってるのがわかる。

あとは計算

　上からn段、左からk番目の数を求めるには次の計算を解く必要がある。
_n-1C_k-1
今、グリッド数gとn, kの関係から(n, k) = (2g+1, g+1)がわかっているので、
(n-1, k-1) = (2g, g)となる。
よって、さっきの式は
_n-1C_k-1 = _2gC_g
となる。

　コンビネーション_aC_bは
\( _{a} C _{b} = \frac{a!}{b!(a-b)!} \)
で求められるので、
\( \displaystyle _{2g} C _{g} = \frac{(2g)!}{g!(2g-g)!} = \frac{(2g)!}{g!^2} = \frac{ \prod_{k=g+1}^{2g}k}{g!} \)
これを解けばいいということになる。

コード

using System;
using System.Diagnostics;
using System.Numerics;

namespace problem15
{
    class Program
    {
        static void Main(string[] args)
        {
            Debug.WriteLine("Result1 " + RoutesList(20));
            Debug.WriteLine("Result2 " + PascalTriangle(20));
        }

        /// <summary>
        /// 配列を使う方法
        /// </summary>
        static Int64 RoutesList(int gridNum)
        {
            if (gridNum <= 0) return 0;

            Int64[] routes = new Int64[gridNum];

            //1に初期化
            for (int i = 0; i < gridNum; i++)
            {
                routes[i] = 1;
            }

            //グリッド数だけ経路数計算をくりかえす
            for (int y = 0; y < gridNum; y++)
            {
                routes[0] += 1;
                for (int x = 1; x < gridNum; x++)
                {
                    routes[x] = routes[x - 1] + routes[x];
                }
            }

            return routes[routes.Length - 1];
        }

        /// <summary>
        /// パスカルの三角形から導く方法
        /// </summary>
        static BigInteger PascalTriangle(int gridNum)
        {
            if (gridNum <= 0) return 0;

            BigInteger m = AllProduct(1, gridNum);
            BigInteger c = AllProduct(gridNum + 1, 2 * gridNum);

            return c / m;
        }

        /// <summary>
        /// 総乗を求める
        /// </summary>
        /// <param name="start">開始する数</param>
        /// <param name="end">終了する数</param>
        /// <returns></returns>
        static BigInteger AllProduct(int start, int end)
        {
            BigInteger ap = 1;

            for (BigInteger i = start; i <= end; i++)
            {
                ap *= i;
            }

            return ap;
        }
    }
}